Complexity

When we talk about algorithmic complexity, there are two main types:

1. Time complexity (Relative according to a metric)
2. Space complexity (memory usage)

Space Complexity

How much memory do we need to run the algorithm?

Here’s an example:

Take an array-like input of size n

[ 0, 1, 2, 3, 4, ..., n-1 ]

For finding something like a max, it takes a constant amount of storage. This is known as an in-place algorithm.

In the “big O” notation, an “in place” algorithm looks like O(k) where k is just some constant (like 5).

Time Complexity

What happens when data is large?

With the same example of an array-like input of size n

[ 0, 1, 2, 3, 4, ..., n-1 ]

We might ask: How much work does an algorithm do in relation to n?

To answer this, we take a key operation (like sort, swap, mult, etc) that’s “inside the loop”. We then count how many times it occurs relative to n.

In general, constant time (or “in place” complexity) is the fastest, and exponential like some number to the power of n is the slowest.

Here’s a graph:

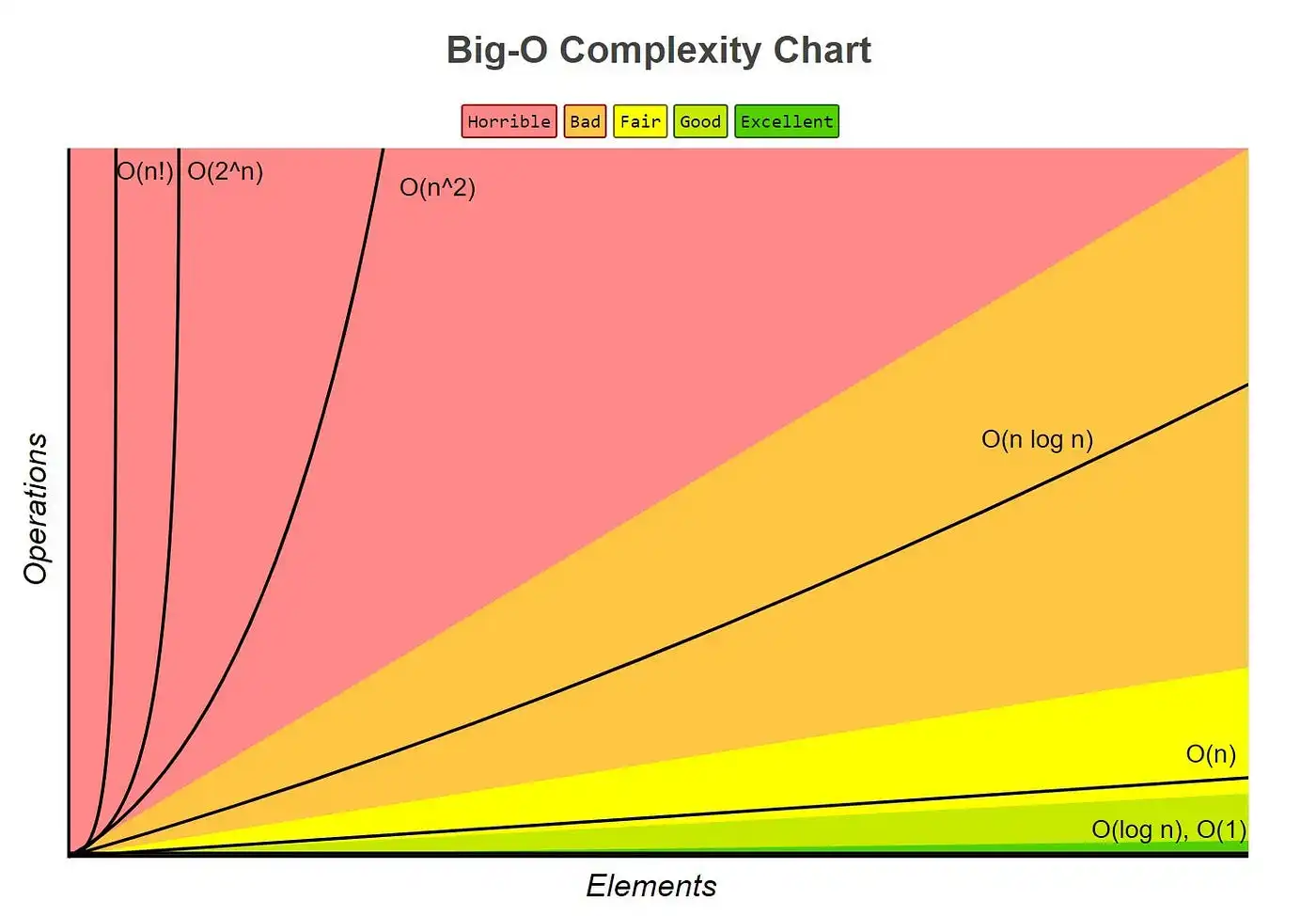
Example Algorithmic Complexity

O(1) <- Insertion into a Set
O(n) <- Linear Search
O(logn) <- Binary Search
O(nlogn) <- Merge Sort
O(n^2) <- Selection Sort, Bubble Sort, Insertion Sort

Practical Example

The basic idea is that coefficients and smaller powers are ignored.

O(n) and O(5n) are going to be so close that the difference is negligible.

The notation O() typically represents the maximum time complexity or the worst possible outcome.

Here’s a real-world example:

Let’s say there are two programmers at a company and the company will fire one of the two due to budget cuts.

Programmer A is good at optimizing and overall writes clean efficient code. He shows up on time and is attentive. He writes code that does 1 billion instructions per second. For the task at hand, he chooses to use a sorting algorithm called insertion sort.

Programmer B is always late to work and overall writes short code, but to the point. He understands programming on a deep level and knows things like when to use '\n' vs std::endl in C++. His code runs 10 million instructions per second. For this task, programmer B uses merge sort.

Given the task of sorting 10 million values, programmer B’s program takes 20 minutes. Whereas programmer A takes 2.3 days.

Unfortunately, despite programmer A being an overall better employee, writing clean code, and showing up on time. Programmer B kept his job due to knowing how to use the more efficient algorithm.